Data: 28/04/2020 - Professora: Maria Batista - Disciplina: Matemática - Conteúdo:Raiz Quadrada Aproximada

ü  Bom dia!

ü  Leiam as instruções abaixo com atenção.

Ø  Façam o cabeçalho e colocando o nome de maneira legível, no início da atividade.

Ø  Assistam a vídeo aula antes de iniciar a leitura do texto e exercícios.

Ø  Copie o texto e exercícios.

Ø  Procurem resolver os exercícios até as 15h00min, para ganhar o visto de caneta preta.

Ø  Escreva de maneira legível, para que eu possa fazer um trabalho melhor.

Ø  Mandem as atividades depois de prontas no privado obedecendo aos horários de vistos.

Ø  Para quem não enviou poderá enviar até às 17h00min, para ganhar os visto de caneta vermelha.

Ø  Às dúvidas podem ser enviadas no grupo ou  no privado.

Lembrem-se de que essas atividades valerão a nota bimestral. Caso o aluno não faça as atividades, o mesmo ficará sem nota. Estarei aqui até as 17:00 para atendê-los

Assista o vídeo abaixo para iniciarmos nossos estudos.

https://www.youtube.com/watch?v=zcIqxlwOopU

Raiz Quadrada Aproximada

Raiz quadrada aproximada de um número é calculada utilizando a estimativa, que é o processo pelo qual conseguimos aproximar valores numéricos. Adotamos esse procedimento para calcular raiz quadrada não exata, que ocorre quando o radicando não é um número quadrado perfeito. Lembre-se que:

• Radicando é o número que fica dentro do radical, ou seja:

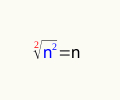
2 = Índice     2 = Expoente     n = Radicando     n = Raiz

• Número quadrado perfeito é obtido pelo produto de um número por ele mesmo. Sendo assim, é todo e qualquer número que tem como expoente o número 2.
  Número           Número quadrado perfeito
  0           →           02 = 0
  1           →           12 = 1
  2           →           22 = 4
  3           →           32 = 9
  4           →           42 = 16
  5           →           52 = 25...
  
  
• A raiz exata de um número é dada por um outro número que é quadrado perfeito.

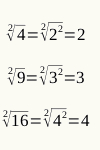
Temos que 4, 9 e 16 são números quadrados perfeitos.

• Para sabermos quando utilizar o processo de estimativa pra calcular raiz quadrada, basta o valor numérico referente ao radicando não ser um número quadrado perfeito. Veja alguns radicais que não são quadrados perfeitos:
  

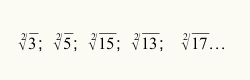
Como já trabalhamos os conceitos iniciais necessários para poder compreender melhor o que é raiz quadrada aproximada, podemos agora determinar o processo pelo qual é realizada a estimativa.

A aproximação para raiz quadrada adota o conjunto dos números racionais. Sendo assim, o valor numérico da raiz sempre será um número com uma ou mais casas decimais. O processo referente à aproximação de raiz quadrada pode ser caracterizado por três passos. Para determinar esses passos vamos calcular a raiz quadrada do número 7.

Primeiro passo

Devemos definir o número quadrado perfeito que é antecessor e sucessor do número 7.

22 < 7 < 32

4 < 7 < 9

Segundo passo

Determinar o possível intervalo que será raiz de 7 e fazer a estimativa variando as casas decimais.

Conseguimos determinar que o número 7 está entre os números quadrados perfeitos 4 e 9. Então o número que será a raiz de 7 está entre 2 e 3. Agora devemos aplicar o processo da estimativa, para isso variamos os números refentes à casa decimal.

(2,1) . (2,1) = (2,1)2 = 4,41

(2,2) . (2,2) = (2,2)2 = 4,84

(2,3) . (2,3) = (2,3)2 = 5,29

(2,4) . (2,4) = (2,4)2 = 5,79

(2,5) . (2,5) = (2,5)2 = 6,25

(2,6) . (2,6) = (2,6)2 = 6,76

(2,7) . (2,7) = (2,7)2 = 7,29

Terceiro passo

Definir qual dos valores da estimativa é raiz

Quando o produto de um número por ele mesmo ultrapassa o valor do radicando que queremos encontrar, paramos de estimar esse número. O que precisamos fazer agora, no caso da raiz quadrada de 7, é decidir se a raiz é o número 2,6 ou 2,7. Por convenção, temos que a raiz de 7 é dada pelo menor valor. Sendo assim:

Para poder fixar melhor este conteúdo faremos mais um exemplo:

Calcule a raiz quadrada do número 21.

42 < 21 < 52

16 < 21 < 25

O número que será raiz de 21 está entre 4 e 5.

(4,1) . (4,1) = (4,1)2 = 16,81

(4,2) . (4,2) = (4,2)2 = 17,64

(4,3) . (4,3) = (4,3)2 = 18,49

(4,4) . (4,4) = (4,4)2 = 19,36

(4,5) . (4,5) = (4,5)2 = 20,25

(4,6) . (4,6) = (4,6)2 = 21,16

Como, por convenção, devemos pegar o menor número para raiz, temos que a raiz de 21 é 4,5.

Exercícios

01-Qual a medida da diagonal de um quadrado cuja área mede 450 cm²?

a) 30 cm

b) 15·√2 cm

c) √2 cm

d) 15 cm

e) 45 cm

02-Em determinada época do ano, a sombra projetada no chão, em um horário próximo ao pôr do sol, é exatamente o quadrado da altura do objeto que projeta essa sombra. Sabendo que o comprimento da sombra de um prédio é de 1728 metros, qual das opções a seguir mais se aproxima de sua altura?

a) 60 metros

b) 50 metros

c) 40 metros

d) 30 metros

e) 20 metros

03-Uma cerca é composta de três paredes, duas iguais que medem √48 m e uma que mede √18 m. Qual é o perímetro aproximado dessa cerca?

a) 6,8 metros

b) 4,2 metros

c) 11 metros

d) 15 metros

e) 17,8 metros


04- Calcule raiz quadrada: exata dos seguintes números racionais na forma fracionária. a) √9/16=

 b) √1/25=

 c) √9/25

d) √16/49 =

e) √64/25=

 f) √1/9=

 g) √25/81=

 h) √49/36=

 i) √1/100=

05-Calcule  a melhor aproximação da raiz cúbica de 864?

06- Determine as raízes:

a) √4 =

b) √25 =

c) √0 =

d) -√25 =

 e) √81 =

 f) -√81 =

g) √36 =

 h) -√1 =

 i) √400 =

 j) -√121 =

k) √169 =

 l) -√900 =

07- Calcule:

 a) √25 + √16 =

 b) √9 - √49 = 

c) √1 + √0 =

d) √100 - √81 + √4 =

 e) -√36 + √121 + √9 =

f) √144 + √169 -√81

08- Calcule

a) 10.√4 = 

b) 3 + √25 = 

c) 1 - √4/9 =

d) √81-√9 =

e) √100 - √25 = 

f) √25/36 - √1/9 = 

g) 4 . √4/100 = 

09- Se √x = 30, então o valor de x é:

a) 60

b) 90

c) 600

d) 900 

10- O valor de expressões √0 + √1 - √1/4 é:

a) 1/4

b) 3/2

c) 1/2 

d) 3/4

11- O valor da expressão 7² - √64 + 3² é:

a) 42
c) 50 

b) 51

d) 38